Exact Complexity Reduction of Constrained Zonotopes for Reachability and Control

This work studies exact complexity reduction of constrained zonotopes, a set representation widely used in reachability analysis, invariant set computation, and verification of constrained dynamical systems. While constrained zonotopes offer expressive and compact representations, their complexity grows rapidly under common set operations such as Minkowski sums, intersections, and Pontryagin differences. This paper addresses the problem of reducing this complexity without introducing approximation error, which is critical for safety-critical control and verification applications.

The paper identifies multiple sources of redundancy in constrained zonotopes and proposes three complementary algorithms to remove these redundancies exactly. The algorithms target redundant generators, redundant factors, and redundant equality constraints while preserving the exact geometry of the represented set.

Algorithm Overview

Algorithm 1 performs redundancy detection using iterative bound refinement on the factor variables. Algorithm 2 guarantees exactness by formulating redundancy checks as linear feasibility problems. While both methods are effective in specific regimes, they either sacrifice exactness or incur high computational cost.

The primary contribution of the paper is a hybrid complexity reduction algorithm that combines fast pre-refinement with selective feasibility checking, achieving exact reduction with significantly improved computational efficiency.

Proposed Algorithm: Hybrid Pre-Refinement and Feasibility-Based Reduction

The proposed algorithm exploits structural properties of constrained zonotopes to eliminate obvious redundancies early, before invoking expensive optimization-based checks. By reordering the reduction process, the algorithm minimizes the number of feasibility problems that must be solved while still guaranteeing exactness of the resulting set representation.

Pseudocode

Input:
    Constrained zonotope Z = { c + Gξ | Aξ = b,  ||ξ||∞ ≤ 1 }

Output:
    Reduced constrained zonotope Z_reduced with identical geometry

Algorithm:
    Initialize:
        Active factor set F ← {1, 2, ..., p}
        Constraint set C ← equality constraints Aξ = b

    Step 1: Pre-refinement
        For each factor ξ_i in F:
            Compute conservative bounds [l_i, u_i] using equality constraints only
            If [l_i, u_i] ⊂ (-1, 1):
                Substitute ξ_i using Aξ = b
                Remove ξ_i from F
                Update generator matrix G and constraints C

    Step 2: Feasibility-based verification
        For each remaining factor ξ_j in F:
            Solve feasibility problem:
                maximize ξ_j subject to Aξ = b, ||ξ||∞ ≤ 1
            If infeasible or max ξ_j < 1:
                Mark ξ_j as redundant
                Substitute ξ_j and update G, C

    Step 3: Final consistency check
        Remove zero generators and dependent constraints
        Re-index remaining factors

Return:
    Z_reduced = { c + G_reduced ξ | A_reduced ξ = b_reduced, ||ξ||∞ ≤ 1 }

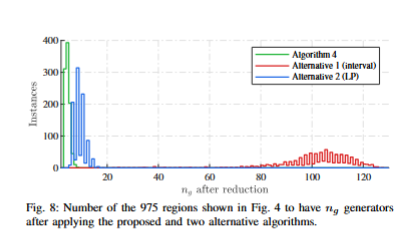
Numerical evaluations demonstrate that the proposed hybrid algorithm consistently achieves the lowest-order exact representations while significantly reducing computation time compared to existing approaches. In applications such as neural network reachability, maximal invariant set computation, and robust model predictive control, the algorithm enables exact set propagation at scales that were previously computationally prohibitive.

By enabling fast and exact complexity reduction, this work makes constrained zonotopes practical for large-scale control, verification, and optimization problems. The proposed algorithm directly supports modern applications involving hybrid systems, neural networks, and safety-critical autonomous systems.