MPC Based Drone Path Optimization and Obstacle Avoidance

This project formulates drone navigation as a constrained optimization problem solved online using Nonlinear Model Predictive Control. At each control step, the controller solves a finite horizon nonlinear program to compute an optimal sequence of acceleration and yaw rate commands that move the drone toward a target while respecting nonlinear dynamics, actuator limits, energy usage, and obstacle avoidance constraints. The optimization is solved using MATLAB FMINCON with an SQP method, enabling direct handling of nonlinear constraints without linearizing the model.

The state includes planar position, velocity, heading, and an energy variable that decreases with the squared control effort, which allows the optimizer to explicitly trade off fast arrival versus energy efficient motion. The objective uses quadratic tracking penalties over the horizon plus a terminal cost, with additional weighting to prevent overshoot near the goal and to encourage physically realistic deceleration as the drone approaches the target.

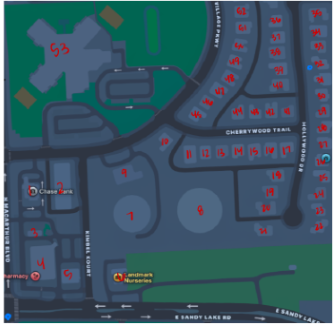
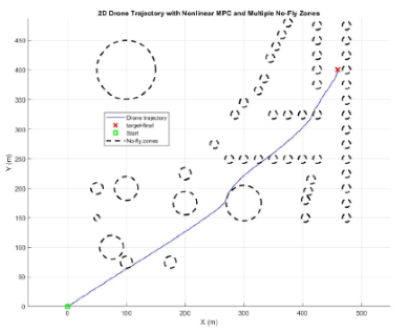
Obstacle avoidance is enforced through nonlinear inequality constraints using circular no fly zones derived from a real neighborhood map. Each building footprint is conservatively approximated as a circle, which keeps the constraints smooth for SQP while still being safety oriented. A buffer term inflates obstacle radii to maintain clearance margins in dense urban like layouts. Because the environment contains more than fifty obstacles, the optimization must satisfy thousands of inequality constraints at each step.

The MPC loop is implemented modularly in MATLAB, with separate dynamics, cost, and constraint functions. To improve convergence and reduce computation time, the previous optimal control sequence is shifted forward and used as the next initial guess. Collision checking is also performed with sub stepping between horizon nodes to prevent the optimizer from numerically slipping through obstacles between discrete prediction points.

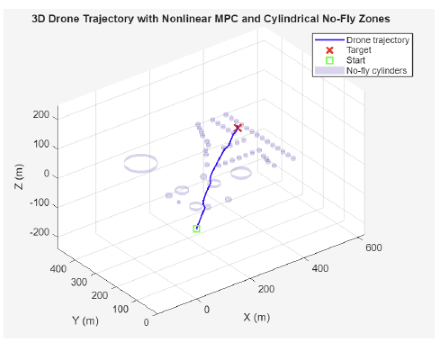
Results show the controller generates smooth, collision free trajectories through highly constrained corridors and adapts speed and heading based on obstacle density. Solve time stays within a practical range for most steps, with peaks occurring in the densest regions where the solver must satisfy many competing constraints. The same formulation was also extended to a preliminary 3D scenario using cylindrical no fly zones, demonstrating scalability toward full 3D planning and future real time NMPC improvements. The horizon of N=15 was used for this project and the robustness was defined by using the buffer regions. Instead of using buffer regions, tube-MPC can also be used for a robust performance.